Long-form generative art
Art Blocks
The project was uploaded on the Ethereum blockchain through Art Blocks and launched on May 2nd, 2022. A total of 300 outputs were minted and will live permanently and immutably on chain along with the script that generated them. Presently some of the mints can be purchased through secondary marketplaces like Archipelago and OpenSea. Notice however that the images appearing on this page are local test outputs and not among the 300 official outputs.


















The Concept
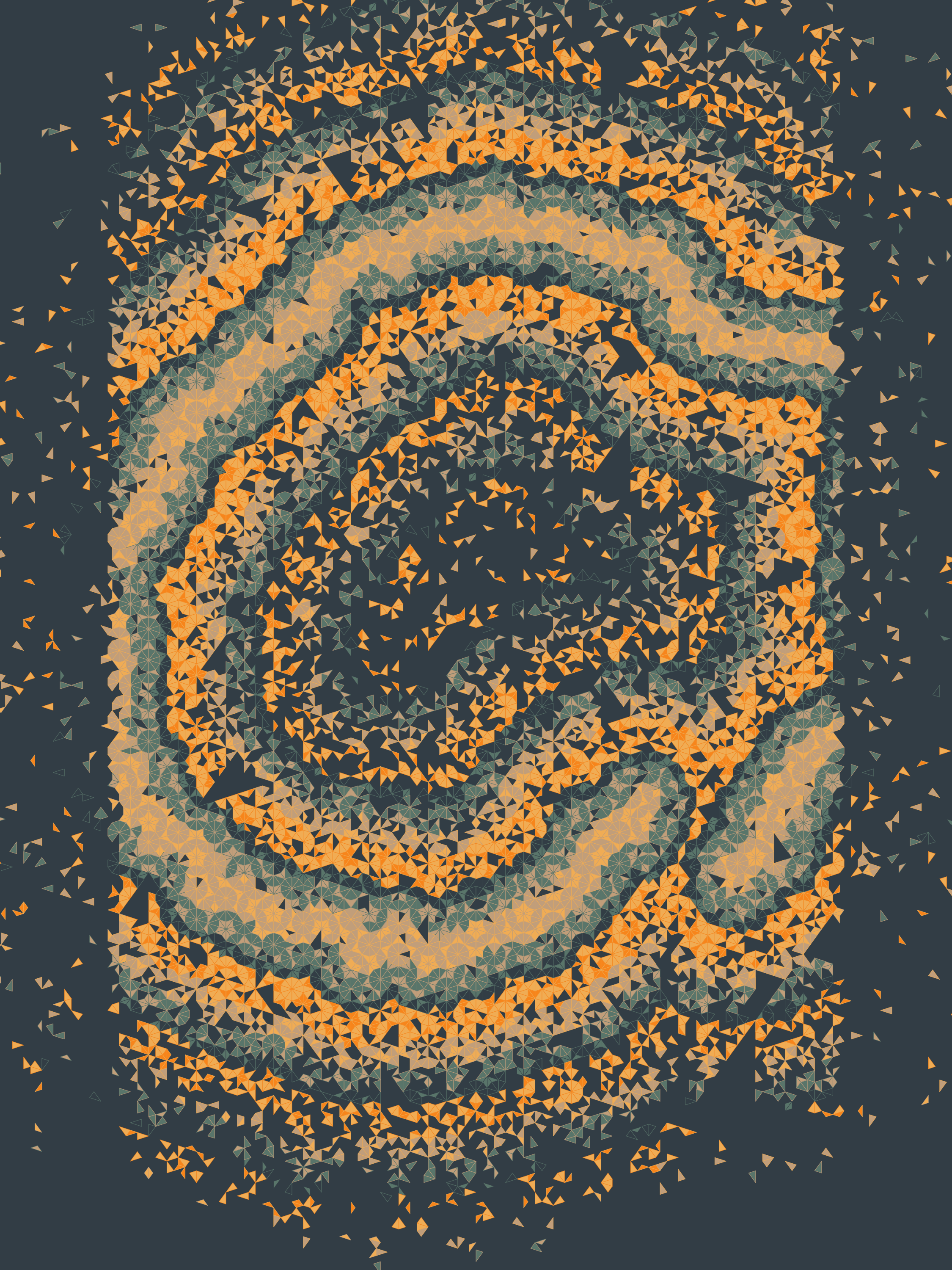
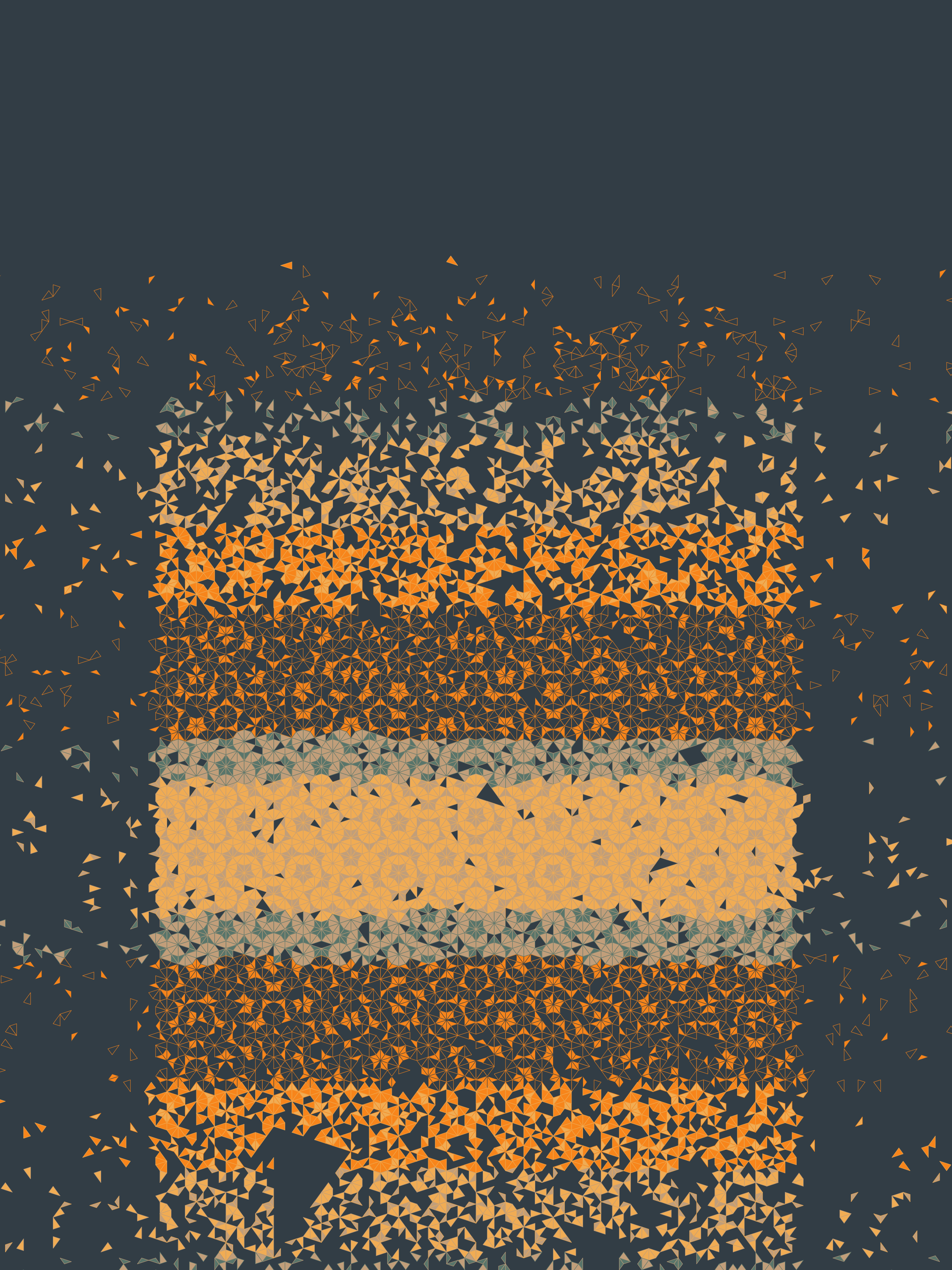
Ode to Penrose explores the intersection of mathematics, computer science and art. The project is a celebration of the discovery and the beauty of aperiodic tilings, specifically of those discovered by Sir Roger Penrose. Tilings often form aesthetically pleasing patterns. Consequently they have been used in fine art and decorative art for thousands of years. For instance M. C. Escher incorporated tilings in many of his paintings. On the other hand for example Islamic tiles can be found decorating walls, ceilings and floors all around the world. Particularly these can be often found in the Middle East, parts of Asia, North Africa and Southern Spain.
Meanwhile aperiodic tilings are an interesting special case. They were discovered as a result of studying a particular problem in mathematics and computer science. They are the main focus of this project. The script uses only two types of triangles as the main building block and some constraints derived from the tiling rules. Stochasticity allows the script to output a variety of visually striking outputs, which could be described as unfinished tilings. Surprisingly, each output could be completed into a traditional Penrose tiling without erasing any lines.
The History
Decision problems
A decision problem is a problem in computability theory that can be formulated as a yes–no question concerning a set of elements. The problem is decidable if there exists a computer algorithm that gives the correct answer for any given input. If such a program does not exist, then the problem is undecidable.
A simple example of a decidable problem is “Given a finite string, does a letter ‘a’ appear at any index?”. The algorithm that gives a correct answer simply iterates through all the indices and compares the content of each index with the letter ‘a’. If it finds one, then it answers “yes”. Otherwise it answers “no”.
On the other hand there exists problems that are undecidable. A famous example of those is the Halting Problem, which asks if a given algorithm ever stops computing with a given input. This problem was proven to be undecidable in 1936 by Alan Turing. Nowadays decision problems are a subject of active research by mathematicians and computer scientists.
Tilings
Tilings or tessellations have been used for decorative purposes for millennia. In fact the earliest known civilization founded in the region of Mesopotamia, Sumer (4500 BC – 1900 BC), were known to have decorated their homes and temples with tilings made from clay. Since then many other civilizations have used tilings as decorations. Hence decorative tilings can be found often for example in walls, pavements and vases all around the world.
Tilings and their properties have been widely studied over the past several decades. In mathematics a tiling is a covering of the whole Euclidean plane without caps or overlaps using a finite set of tiles. A tiling is periodic if we can take a copy of the tiling, translate it towards some vector in such a way that it coincides with the original tiling. On the other hand a tiling is aperiodic if such a vector does not exist. A tile set is aperiodic if each tiling formed from it is aperiodic.
Aperiodic tilings
A tiling problem is a decision problem asking if for a given finite set of tiles, there exists a valid tiling or not. Hao Wang first proposed this problem in the special setting of Wang tiles in 1961. While he did not prove this problem himself, he found an algorithm that could answer this question if aperiodic tile sets didn’t exist. However his student Robert Berger showed that the problem was undecidable in 1964, which consequently also implied the existence of aperiodic tile sets.
Therefore the discovery of aperiodic tilings has its historical roots tied in algorithms and decision problems. Aperiodic tilings remind us of limitations of computers, particularly there are some problems they can not solve.
The first discovered aperiodic tile sets were complicated and they contained thousands of tiles. Since the 1960s researchers discovered smaller and smaller tile sets. Specifically Roger Penrose discovered several small tile sets. One of them consists of only two tiles named kite and dart and is the foundation of this project.
The Details
The script decides a focal point for each output, and then draws invisible shapes on the canvas, which affect the overall structure. Those shapes then influence how the Penrose tiles are used to fill the canvas. There are twelve main shapes that can be filtered by the proximity vector. How the tiles are then placed is affected by the realization and the substitution method. Tiles can either be same size everywhere or larger when distant from the focal point. The probability of tiles being drawn or not is also affected by the focal point.
There are 25 palettes, which I named based on moods I associated them with. The way the script colors the tiles using said palettes is controlled by the co-operation of the focal point and other sources of randomness. The scripts may also sometimes shift colorings on random vertical strips around the canvas.
Using these methods, the script draws hundreds of thousands tiles on the canvas into aesthetically pleasing compositions.



















